凌晨十分，自己的服务监控系统报警说acmore.cc有大批提交卡在正在运行状态无法评测，我第一反应是自己的代码出现了bug，本来有些无奈又有些高兴，心想不知道是哪位高手又爆出了我的代码bug。
熟练的打开IDE，远程近家里的Runner服务器，奇怪的事情发生了。
开发环境下的代码运行一切正常，远程Runner总是出现问题，查了一下log，发现竟然是Runner无法访问阿里云的重要的基础服务OSS储存！！！
我刚开始以为是家里的宽带服务出现了问题，毕竟我实在拿家用宽带做着一些商用宽带才能做的事情，便重启了一下路由器，更换了一个公网IP，结果还是无法访问。接着随手找了个站长工具ping了一下oss ip，发现山东联通的线路全部无法访问了。
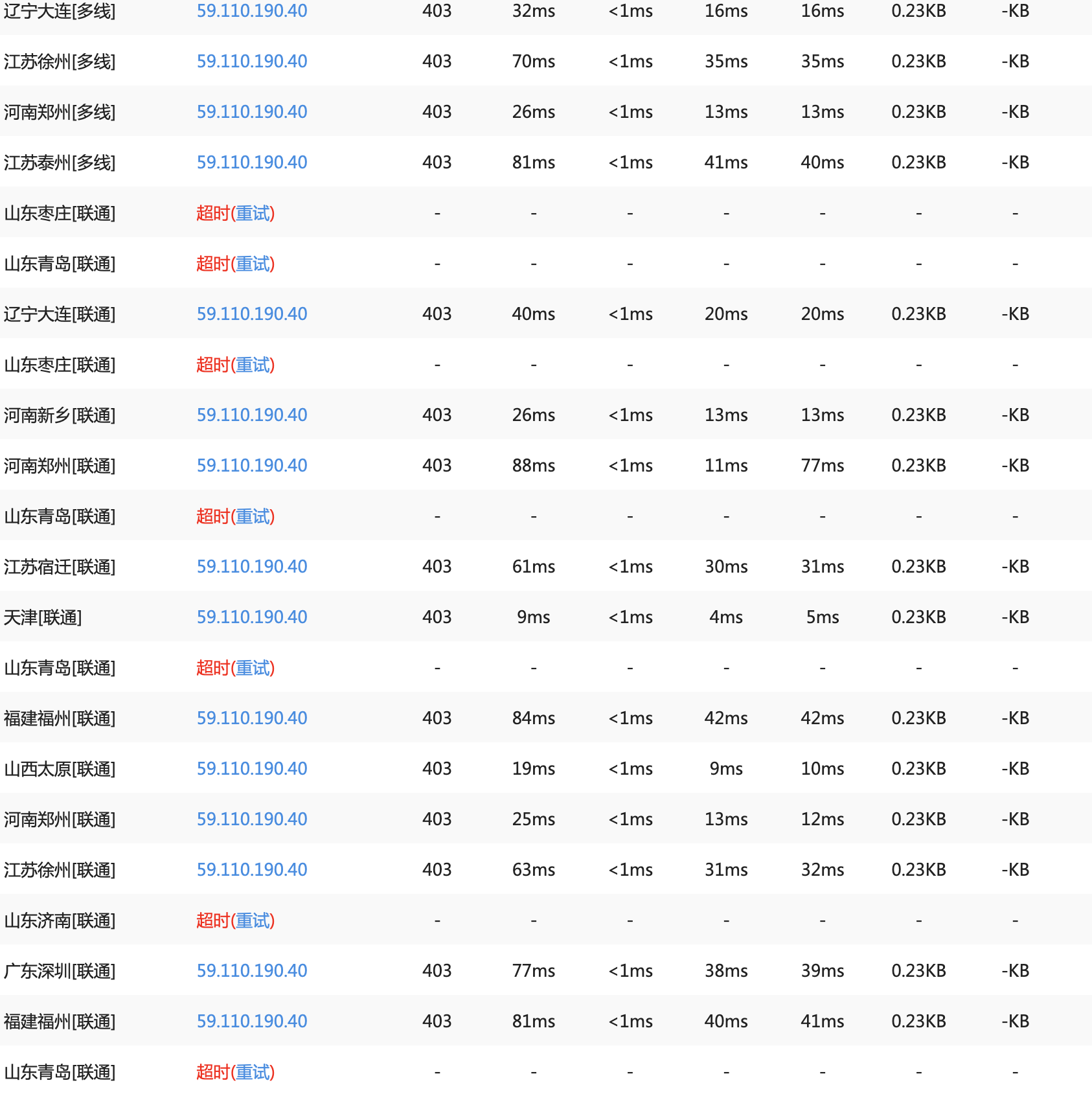
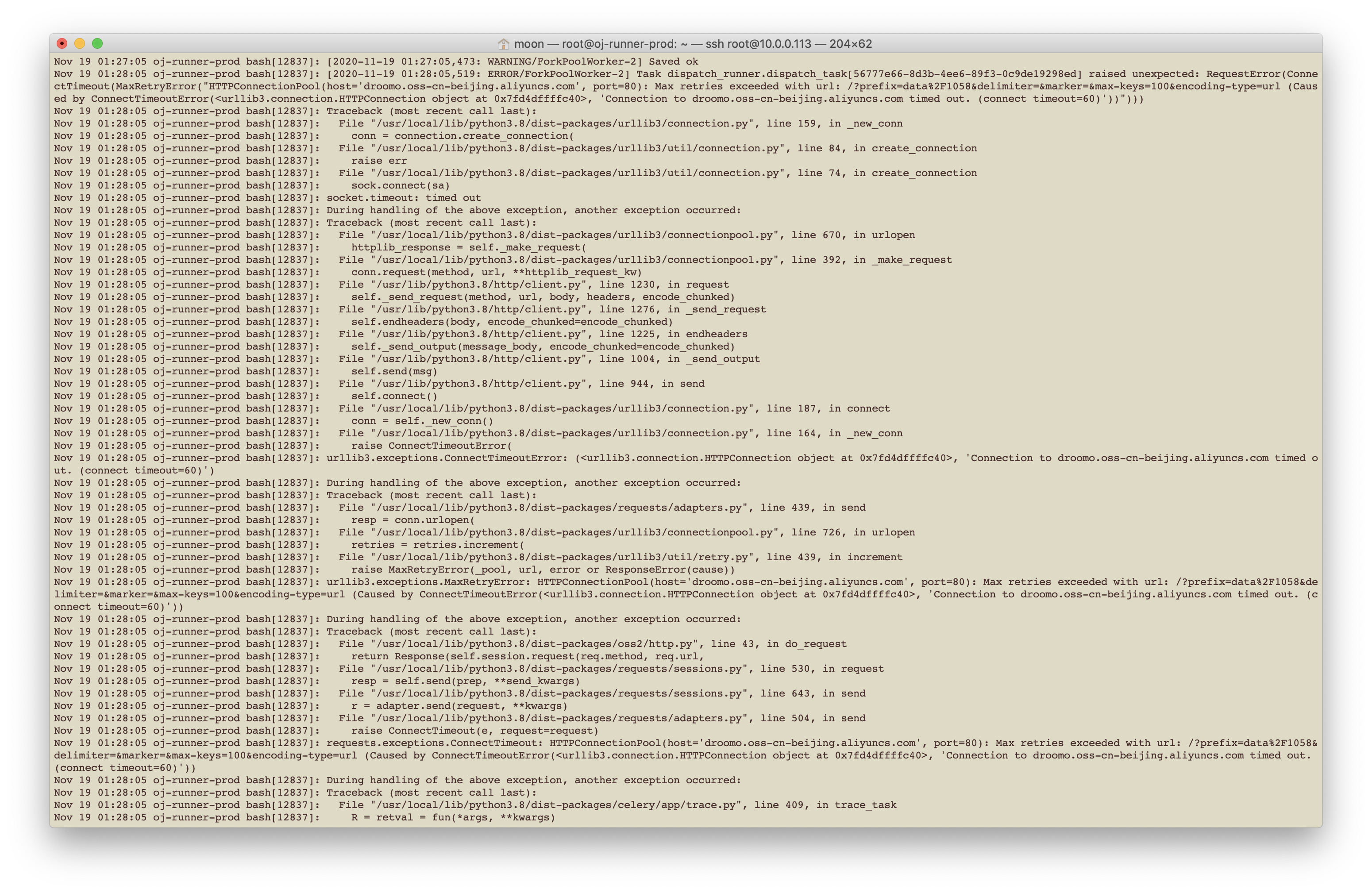
天呐，多么严重的事故！OSS算得上是阿里云提供的非常基础，非常重要的服务，竟然出了如此严重的问题！就像是本来卖西瓜的王婆家，突然西瓜全变成了石头蛋蛋，做生意有这样的吗？？
这还是号称六个九安全性的阿里云？
Pull lastest docker image of onlyoffice server. Then cope new fonts to docker container.
docker pull onlyoffice/documentserver
docker stop office
docker rm office
docker run -i -t -d -p 5580:80 --restart=always --name=office onlyoffice/documentserver
docker cp onlyoffice-fonts office:/usr/share/fonts/truetype/custom
docker ps
docker exec -it office bashRemoving original fonts.
rm -rf /var/www/onlyoffice/documentserver/core-fonts/*
rm -rf /usr/share/fonts/X11
rm -rf /usr/share/fonts/truetype/{* except custom path}Generate new fonts cache.
bash /usr/bin/documentserver-generate-allfonts.shcp -r /var/www/onlyoffice/documentserver/web-apps/apps/documenteditor/main/resources/help/en \
/var/www/onlyoffice/documentserver/web-apps/apps/documenteditor/main/resources/help/zh2020年6月，本插件发布1.1.8版本。
2022年，humu更新插件，支持php8。有需要的朋友请到Github自取。
此版本修复了以前版本的一些BUG，做了一些改善，主要有：
祝使用愉快～
插件名：AliOssForTypecho
作者：droomo
当前版本：v1.1.8
更新时间：2020-06-27
下载地址：https://github.com/droomo/AliOssForTypecho/archive/v1.1.8.zip
百度网盘：https://pan.baidu.com/s/1JeyjeFLLEYd2G4pRcL_O7w 提取码：bum0
Github地址：https://github.com/droomo/AliOssForTypecho
AliOssForTypecho；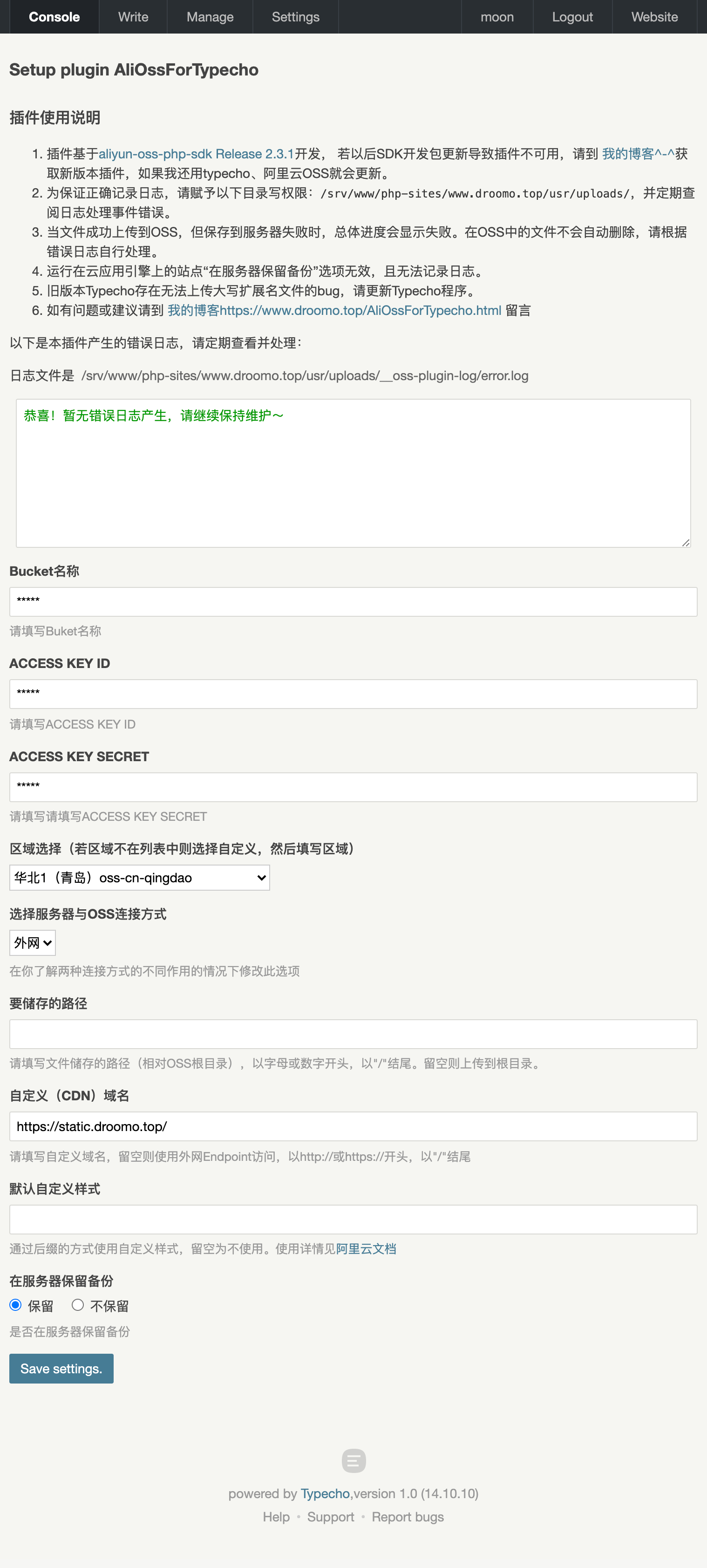
另外针对评论中提议较多的做出一些解释：
Q: 为什么不根据文章id来归档？
A: 因为在上传附件时，插件并无法得到文章信息。根据日期归档是通常做法，与Wordpress保持一致。
People can do almost everything vis ssh under Linux, no exception for CentOS. But in some cases， using a X Windows improves efficiency greatly.
Tiger VNC server is a good server end package for VNC protocal under CentOS.
Tonight, just an hour ago, I encountered a disaster due to an unprofessional systemctl script privided by Tiger VNC server devolopers.
I’m tired so I shall not record the details.
If you are suffering problems while you are deploying autostart VNC server via systemctl, like:
New main PID <pid> does not belong to service, and PID file is not owned by root. Refusing.;Just try a .service file as fllow:
Do !NOT! forget to change USERNAME to your own user.
[Unit]
Description=Remote desktop service (VNC)
After=syslog.target network.target
[Service]
Type=forking
# Clean any existing files in /tmp/.X11-unix environment
ExecStartPre=/sbin/runuser -l <USERNAME> -c '/usr/bin/vncserver -kill %i > /dev/null 2>&1 || :'
ExecStart=/sbin/runuser -l <USERNAME> -c "/usr/bin/vncserver :1"
ExecStartPost=/bin/sh -c '/usr/bin/cat /home/<USERNAME>/.vnc/%H%i.pid > /tmp/vnc-server.pid'
PIDFile=/tmp/vnc-server.pid
ExecStop=/sbin/runuser -l <USERNAME> -c '/usr/bin/vncserver -kill %i > /dev/null 2>&1 || :'
[Install]
WantedBy=multi-user.targetGetting 500 Internal error on /admin/application_settings
https://gitlab.com/gitlab-org/gitlab-foss/issues/56403
Gitlab WEB-IDE: Error while loading project data. please try again.
https://gitlab.com/gitlab-org/gitlab-foss/issues/45657
This issue seems to be caused by the lack of mariadb lib which should have been in the package mariadb-devel.
https://stackoverflow.com/questions/46495448/unable-to-install-mysqlclient-on-centos/46495507
在一段时间以来，我一直使用轻量级的Gogs作为私有代码仓库。最近一段时间苦于Gogs缺少CI、任务管理等一系列功能，准备将Gogs迁移到Gitlab。
网上找过很多迁移方法只能迁移仓库，issues信息会全部丢失。因此我探索了一个可以完整迁移repos、issues的办法，在此简单记录迁移过程，不做详细教程。如果你希望从本文中获得帮助，请确保拥有以下知识储备：
绘制所用的Python代码如下：
import matplotlib.pyplot as plt
from scipy import linspace, sqrt
from scipy.special import erf
import numpy as np
color = '#339999'
color2 = '#660033'
def pdf(x, mu=0, sigma=1):
"""
Calculates the normal distribution's probability density
function (PDF).
"""
term1 = 1.0 / (sqrt(2 * np.pi) * sigma)
term2 = np.exp(-0.5 * ((x - mu) / sigma) ** 2)
return term1 * term2
def cdf(_x):
return (1 + erf(_x / sqrt(2))) / 2
def skew(_x, e, _w, a, z=100):
t = (_x - e) / _w
return z / _w * pdf(t) * cdf(a * t)
plt.figure(figsize=(20, 10))
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
n = 129
w = 2.5
y_text_offset = -0.5
y_title_offset = 8.1
fontsize = 24
middle_x = 0
x = linspace(middle_x - w * 3.3, middle_x + w * 3.3, n)
p = skew(x, middle_x, 3, 0)
plt.plot(x, p, 'r-', color=color, linewidth=3.0)
middle_index = list(p).index(max(p))
plt.text(x[middle_index + 12] - 0.4, max(p)-0.4, '总体', fontsize=fontsize, color=color)
plt.plot([x[middle_index], x[middle_index]], [0, p[middle_index]], '--', color=color,
linewidth=3.0)
plt.text(x[middle_index] - 0.1, y_text_offset, '$\mu$', fontsize=fontsize, color=color)
plt.ylim([0, max(p) + 0.2])
middle_x = middle_x + 0.4
x = linspace(middle_x - w * 1.5, middle_x + w * 1.5, n)
p = skew(x, middle_x, 1.4, 0, 24)
plt.plot(x, p, 'r-', color=color2, linewidth=3.0)
plt.text(x[middle_index + 12] - 0.4, max(p), '样本', fontsize=fontsize, color=color2)
plt.plot([x[middle_index], x[middle_index]], [0, p[middle_index]], '--', color=color2,
linewidth=3.0)
plt.text(x[middle_index] - 0.1, y_text_offset, r'$\barX$', fontsize=fontsize, color=color2)
print([min(x), max(x)])
plt.plot([min(x), max(x)], [y_text_offset, y_text_offset], 'r-', color=color2,
linewidth=3.0)
plt.title('样本和总体的方差比较', fontsize=fontsize)
plt.yticks([])
plt.xticks([])
plt.show()