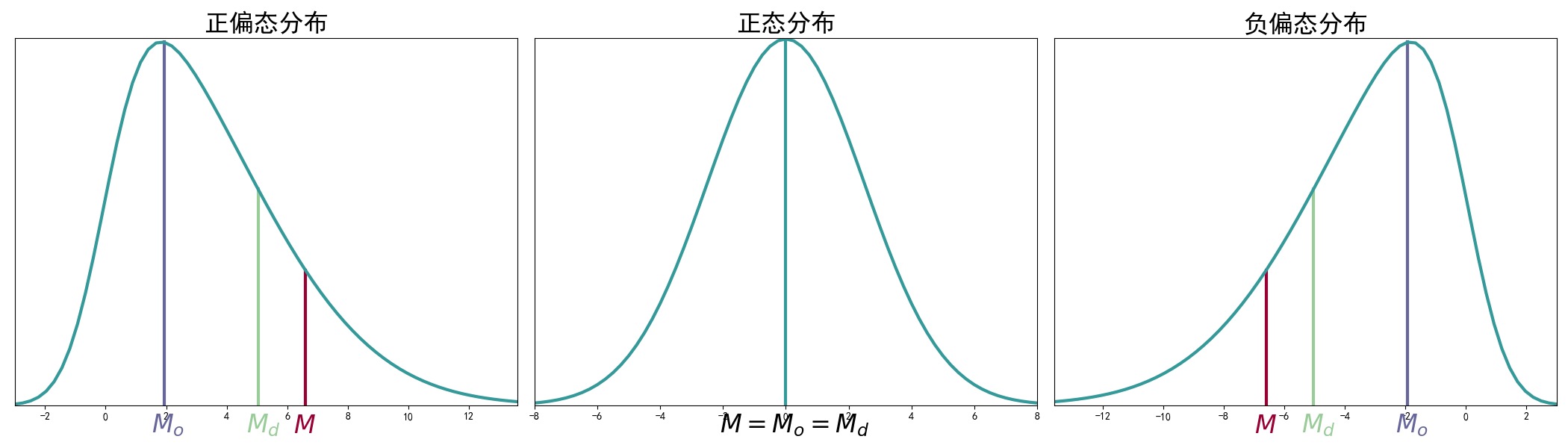
Python绘制上图代码

import matplotlib.pyplot as plt
from scipy import linspace, sqrt
from scipy.special import erf
import numpy as np

color = '#339999'
mean_color = '#990033'
median_color = '#99CC99'
most_color = '#666699'


def pdf(x, mu=0, sigma=1):
    """
    Calculates the normal distribution's probability density
    function (PDF).

    """
    term1 = 1.0 / (sqrt(2 * np.pi) * sigma)
    term2 = np.exp(-0.5 * ((x - mu) / sigma) ** 2)
    return term1 * term2


def cdf(_x):
    return (1 + erf(_x / sqrt(2))) / 2


def skew(_x, e, _w, a):
    t = (_x - e) / _w
    return 100 / _w * pdf(t) * cdf(a * t)


plt.figure(figsize=(21, 6))
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

n = 65
w = 2.5
y_text_offset = -0.6
y_title_offset = 8.1

fontsize = 24

middle_x = 0

plt.subplot(1, 3, 1)
plt.title('正偏态分布', fontsize=fontsize)
plt.yticks([])

x = linspace(middle_x - 3, middle_x + 13.6, n)

plt.ylim([0, 8])
plt.xlim([min(x), max(x)])

p = skew(x, middle_x, 4.4, 4)
middle_index = list(p).index(max(p))
plt.plot([x[middle_index], x[middle_index]], [0, max(p)], 'r-', color=most_color, linewidth=3.0)
plt.plot([x[middle_index + 12], x[middle_index + 12]], [0, p[middle_index + 12]], 'r-', color=median_color,
         linewidth=3.0)
plt.plot([x[middle_index + 18], x[middle_index + 18]], [0, p[middle_index + 18]], 'r-', color=mean_color, linewidth=3.0)
plt.plot(x, p, 'r-', color=color, linewidth=3.0)

plt.text(x[middle_index] - 0.4, y_text_offset, r'$M_o$', fontsize=fontsize, color=most_color)
plt.text(x[middle_index + 12] - 0.4, y_text_offset, r'$M_d$', fontsize=fontsize, color=median_color)
plt.text(x[middle_index + 18] - 0.4, y_text_offset, r'$M$', fontsize=fontsize, color=mean_color)


plt.subplot(1, 3, 2)
plt.title('正态分布', fontsize=fontsize)
plt.yticks([])

x = linspace(middle_x - w * 3.2, middle_x + w * 3.2, n)
plt.ylim([0, 8])
plt.xlim([min(x), max(x)])

p = skew(x, middle_x, w, 0)
middle_index = list(p).index(max(p))
plt.plot([x[middle_index], x[middle_index]], [0, max(p)], 'r-', color=color, linewidth=3.0)
plt.plot(x, p, 'r-', color=color, linewidth=3.0)

plt.text(middle_x - 2.1, y_text_offset, r'$M=M_o=M_d$', fontsize=fontsize)


plt.subplot(1, 3, 3)
plt.title('负偏态分布', fontsize=fontsize)
plt.yticks([])
plt.ylim([0, 8])

x = linspace(middle_x - 13.6, middle_x + 3, n)
plt.ylim([0, 8])
plt.xlim([min(x), max(x)])

p = skew(x, middle_x, 4.4, -4)
middle_index = list(p).index(max(p))
plt.plot([x[middle_index], x[middle_index]], [0, max(p)], 'r-', color=most_color, linewidth=3.0)
plt.plot([x[middle_index - 12], x[middle_index - 12]], [0, p[middle_index - 12]], 'r-', color=median_color,
         linewidth=3.0)
plt.plot([x[middle_index - 18], x[middle_index - 18]], [0, p[middle_index - 18]], 'r-', color=mean_color, linewidth=3.0)
plt.plot(x, p, 'r-', color=color, linewidth=3.0)

plt.text(x[middle_index] - 0.4, y_text_offset, r'$M_o$', fontsize=fontsize, color=most_color)
plt.text(x[middle_index - 12] - 0.4, y_text_offset, r'$M_d$', fontsize=fontsize, color=median_color)
plt.text(x[middle_index - 18] - 0.4, y_text_offset, r'$M$', fontsize=fontsize, color=mean_color)

plt.show()